Cálculo Electoral presenta un agregador de encuestas y un modelo de pronóstico electoral para las elecciones presidenciales de Ecuador. Algunos de los métodos que empleamos son tomados del trabajo que Nate Silver realizó en 538. Aquí describimos paso a paso de donde vienen los números que publicamos.
1. Agregador de Encuestas
La intención de voto de cada candidato (a la fecha de la última encuesta disponible) se lo obtiene siguiendo los siguientes cuatro pasos: recopilación de información, cálculo de ponderaciones para cada encuesta, homologación de resultados y estimación del promedio de intención de voto.
1.1. Recopilación de Información
Prestaremos particular atención a aquellas encuestas con alcance nacional y que hayan referido información completa de datos en todas las categorías de respuesta, incluyendo voto blanco y nulo. En caso de que surgieran otras fuentes de información publicadas en medios de comunicación o portales institucionales de encuestadoras, dichas fuentes serán incorporadas al modelo siempre y cuando provengan de empresas registradas en el Consejo Nacional Electoral (CNE), o si son entidades internacionales de investigación con trayectoria comprobable y con participación previa en elecciones ecuatorianas.
1.2. Cálculo de Ponderaciones
Para poder calcular un promedio ponderado, debemos primero asignar pesos a cada encuesta. Utilizamos una escala de 100 puntos para calificar a cada encuesta con base a los siguientes cuatro criterios:
- - técnica utilizada para entrevistar,
- - cobertura del universo de la muestra,
- - capacidad para predecir la Elección Presidencial Ecuador 2021 (para la Segunda Vuelta, utilizamos los resultados del 20 de agosto de 2023), y
- - actualidad de la encuesta (número de días antes de las elecciones).
Los tres primeros criterios aportan equitativamente con 33.3 puntos, y están relacionados con la calificación de la encuestadora. El primer criterio otorga una calificación según la técnica utilizada para levantar las encuestas, de acuerdo a una categorización de las herramientas generalmente utilizadas: papeleta simulada, entrevistas cara a cara, entrevistas telefónicas, o formulario en internet. En el segundo criterio, damos mayor ponderación a las encuestadoras cuyos datos publicados dan cuenta de levantamientos de muestra a nivel nacional, versus encuestadoras con coberturas regionales. Para el tercer criterio, calculamos el valor absoluto de las diferencias entre el último sondeo de cada encuestadora (excluyendo el exit poll) y el resultado final de la Primera Vuelta para cada candidato en las Elecciones Presidenciales de 2021. El complemento entre el promedio de estas diferencias y 100% nos da una medida de la capacidad de predicción global para la elección en unidades de intención de voto. A la capacidad de predicción la normalizamos con respecto a 33.3, calificación que es obtenida por la empresa encuestadora con el menor error absoluto medio.
El último criterio es utilizado para tomar en cuenta la proximidad temporal de cada encuesta al día de la elección. A la suma de los 3 primeros criterios le multiplicamos por una función exponencial que hace las veces de filtro temporal. La constante de tiempo de este filtro se la determina a partir de la evolución temporal del nivel de decisión que reportan algunas encuestadoras. Al parametrizar las curvas del nivel de decisión para estas elecciones, encontramos que la constante de tiempo es de 2 días (para la Primera Vuelta fue de 5 días). Esto quiere decir que una encuesta publicada el día de hoy tendría 2.7 veces más influencia que una publicada hace 2 días.
1.3. Ajustes para Homologar Encuestas
1.4. Promedios Ponderados
El estimado de la intención de voto es el resultado de un promedio con pesos de las encuestas seleccionadas. El promedio se lo realiza individualmente para cada candidato. El momento que conozcamos de algún nuevo sondeo, lo someteremos al procedimiento descrito en los pasos anteriores para poder actualizar el estimado de la intención de voto.
2. Pronósticos
Reportamos pronósticos con base en un análisis de cómo evolucionan las tendencias de cada candidato, y además, estudiamos las principales fuentes de incertidumbre para poder simular la elección miles de veces. Los resultados de estas simulaciones son catalogados de acuerdo a sus diferentes desenlaces, y al contar resultados de similar desenlace (por ejemplo, cuántas veces el candidato ganador supera el 50%), podemos estimar cuál es la probabilidad de que dichos desenlaces ocurran al final de la contienda electoral.
2.1. Cálculo y Ajuste de Tendencias
El modelo hace comparaciones entre diferentes ediciones de la misma encuestadora. Por ejemplo, si Click Research registra que uno de los candidatos tiene un 33% de intención de voto en el mes de julio y obtiene un 36% en una versión de la encuesta con similar metodología durante el mes de agosto, esto sugiere que dicho candidato ganó 3 puntos porcentuales. Si hay suficientes datos, realizamos estas comparaciones para cada candidato y encuestadora por separado. Luego, tomamos estas comparaciones y trazamos una línea de tendencia haciendo uso de una regresión local. Estas tendencias por encuestadora nos ayudan a decidir cómo calcular tendencias globales conforme aparecen nuevos puntos para ser agregados. Cuando esta información no está disponible, hacemos una regresión local directamente sobre los puntos que aparecen en el agregador de encuestas (independientemente de la encuestadora). Procuramos utilizar funciones con pocos parámetros y de bajo orden, para evitar efectos no lineales en extrapolaciones. Nos aseguramos de que el sumatorio de cada punto (en el tiempo) de las líneas de tendencia sume 100%, y que sea posible para cada candidato ganar o perder votos.
Esta metodología fue puesta a prueba por primera vez durante las elecciones presidenciales Ecuador 2017: tanto en la primera vuelta, como en el balotaje. Estos resultados demostraron que el tratamiento que dimos a los datos para homologarlos fue adecuado. Los pronósticos de Cálculo Electoral fueron los que más se acercaron a los resultados de dichas elecciones. También participamos con éxito en las recientes elecciones presidenciales Ecuador 2021, Perú 2021, y Colombia 2022.
2.2. Estimación de la Incertidumbre
El promedio proyectado de intención de voto para cada candidato se lo obtiene a partir de variables que tienen sus propios errores probabilísticos y/o sistemáticos. Estas variables son: 1) la intención de voto por candidato difundida por encuestadoras, y 2) la fracción de indecisos o indeterminados asignada a cada candidato. Para poder estimar la incertidumbre total, utilizamos el modelo simplificado de propagación de errores para funciones no-lineales (en donde se asume variables independientes). Las incertidumbres en las intenciones de voto son proporcionales a la discrepancia que existe entre los datos publicados por las diferentes encuestadoras. La incertidumbre en la segunda variable es proporcional a la fracción asignada a cada candidato.
2.3. Generación de Trayectorias
2.4. Cálculo de Probabilidades
Errores y Omisiones
Intentamos evitar manipular el modelo una vez que se publica, pero siempre estamos atentos a errores. Si hay cambios significativos en el modelo, los divulgaremos aquí.
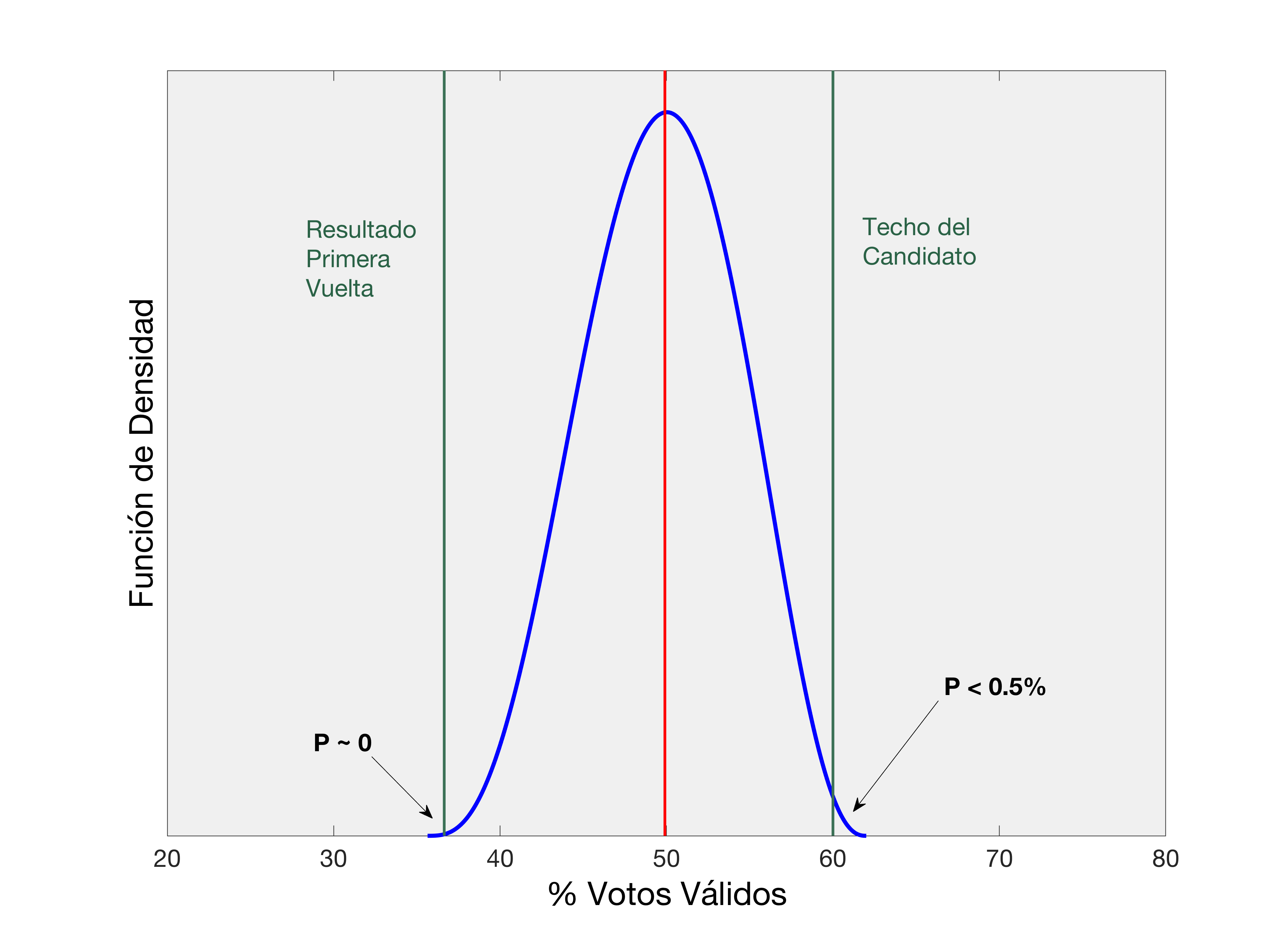
* Consideraremos en un futuro utilizar distribuciones t, ya que teóricamente son más apropiadas cuando las muestras son pequeñas. Además, estas tienen colas más largas que una distribución normal, o una beta (particularmente las distribuciones t con pocos grados de libertad). En este momento es difícil decidir el número de grados de libertad que se debe emplear, ya que no tenemos suficientes datos para saber como se comporta la cola de la distribución. Por ejemplo, ¿cuál es la probabilidad de que un candidato que va perdiendo por 20 puntos en las encuestas termine ganando la elección? La respuesta podría cambiar por varios ordenes de magnitud (1, 0.1 ó 0.01% chances de ganar) dependiendo de cuantos grados de libertad se utilicen en la distribución t. Una distribución t bien parametrizada ayudaría a modelar de mejor manera estos casos extremos.